Boats and Streams Formulas with examples for SSC and Bank Exams

Often students face difficulty while using boats and streams formulas in the competitive exam questions because they don't know the proper way to solve the boats and streams questions or equations. These boats and streams questions usually asked in SSC and bank exams. 

So here in this blog, you can improve your performance to learn how to use boats and streams formulas with examples for competitive exams. You can practice also these boats and streams questions with answers to get the better score in your competitive exams.

Click here to solve problems of boats and streams with sufficient examples to complete question on time in competitive exams. 

Boats and Streams Formulas with Examples for Competitive Exams

Downstream Movement

When the direction of the movement of a river and boat is the same, their collective movement is known as the downstream movement. And the distance covered by boat is known as downstream distance.

If the speed of a boat in still water is x and speed of the stream is y, then downstream speed = x+y

Up stream Movement 

When the direction of the movement of the river and a boat is opposite, they are said to be in upstream movement. The distance covered in this case is known as upstream distance.

If the speed of the river = x and the speed of the boat = y, the upstream speed = x-y

Important Facts  -

1. Still water implies that the speed of water in the river is zero.

2. Stream water implies that the water in the river is moving.

3. If the speed of a down still water is x and speed of the stream is y, then

                     * Speed of downstream = x + y

                     * Speed of Upstream =x-y

                     * Speed of boat in still water(x)=1/2 (Speed downstream + Speed Up stream)

                     * Speed of stream (y) =1/2(Speed downstream - Speed Up stream)

Important Formula -

1. If the speed of a boat in still water is u km/hr and the speed of the stream is v km/hr, then:

Speed downstream = (u+v) km/hr.

Speed upstream = (u-v) km/hr.

2. If the speed downstream is a km/hr and the speed upstream is b km/hr, then:

Speed in still water = 1/2 (a+b) km/hr.

Rate of stream = 1/2(a-b) km/hr.

Solved example 

Ex.1. A man can row upstream at 7 kmph and downstream at 10 kmph. Find man’s rate in still water and the rate of current.

Solution:

Rate in still water = 1/2(10+7) km/hr = 8.5

Rate of current = 1/2(10-7) km/hr = 1.5 km/hr.

Ex.2. A man takes 3 hours 45 minutes to row a boat 15 km downstream of a river and 2 hours 30 minutes to cover a distance of 5 km upstream. Find the spend of the river current in km/hr.

Solution:

Rate downstream = 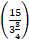 km/hr =  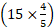km/hr = 4 km/hr.

Rate upstream = 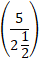 km/hr =  km/hr = 2 km/hr.

∴ Speed of current = (4-2) km/hr = 1 km/hr.

Ex.3. A man can row 18 kmph in still water. It takes him thrice as long to row up as to row down the river. Find the rate of stream.

Solution:

Let man’s rate upstream be x kmph. Then, his rate downstream = 3x kmph

∴ Rate in still water = (3x+x) kmph = 2x kmph.

So, 2x = 18 or x = 9.

∴ Rate upstream = 9 km/hr, Rate downstream=27 km/hr.

Hence rate of = (27-9) km/hr = 9 km/hr.

Ex.4. There is a road beside a river. Two friends started from a place A, moved to a temple situated at another place B and then returned to A again. One of them moves on a cycle at a speed of 12 km/hr, while the other sails on a boat at a speed of 10km/hr. If the river flows at the speed of 4 km/hr, which of the two friends will return to place A first?

Solution:

Clearly, the cyclist moves both ways at a speed of 12 km/hr.

So, average speed of the cyclist = 12 km/hr.

The boat sailor moves downstream @ (10+4) i.e., 14 km/hr and upstream@ (10-4) i.e, 6 km/hr.

So, average speed of the boat sailor $$ =   \left({2×14×6\over14+6}\right)={42\over5} $$

Ex.5. A man can row 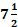 kmph in still water. If in a river running at 1.5 km an hour. It takes him 50 minutes to row to a place and back, how far off is the place?

Solution:

Speed downstream = (7.5+1.5) kmph = 9kmph; 

Speed upstream = (7.5 – 1.5) kmph = 6 kmph,

Let the required distance be x km. Then, 

$$   =  {x\over9}+{x\over6} ={50\over60}↔2x+3x= \left({5\over6}× 8\right)↔5x+15↔x=3$$

Hence, the required distance is 3 km.

You can practice boats and streams problems with help of these formulas. You can ask me anything about boats and streams formulas with examples for ssc and bank exams, if you have any doubt or problem.