Height and Distance formulas with examples for SSC and Bank Exams

Height and Distance Formulas with Examples for Competitive Exams

Ex.6. If the height of a pole is 2√3 metres and the length of its shadow is 2 metres, the angel of elevation of the sun.

$$Solution$$

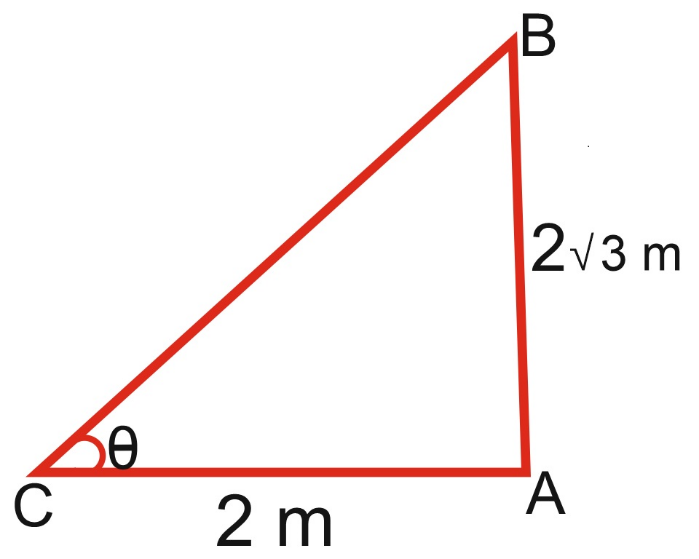
Let AB be the pole and AC be its shadow.

Let angle of elevation, ∠ABC = θ.

Then, AB = 2√3 m, AC = 2 m.

$$tan \ θ = {AB\over AC}={{2}\sqrt{3}\over2}=\sqrt{3}\ ⇒ θ = 60^0 $$

So, the angel of elevation is 60⁰

Ex.7. A ladder leaning against a wall makes an angle of 60⁰ with the ground. If the length of the ladder is 19 m, find the distance of the foot of the ladder from the wall.

$$Solution$$

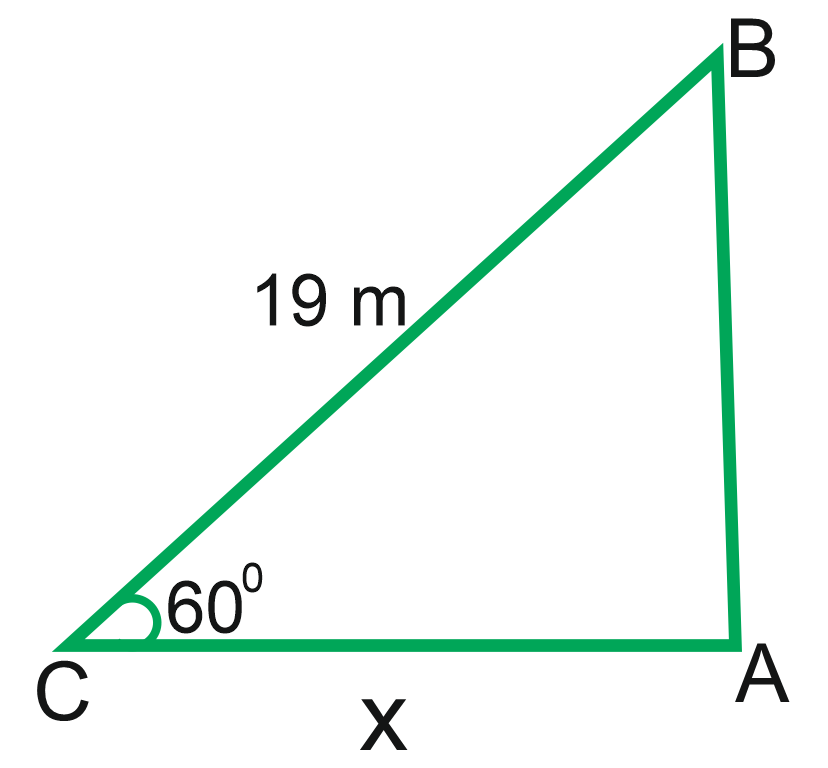
Let AB be the wall and BC be the ladder.

Then, ∠ABC = 60⁰ and BC = 19 m.

Let AC = x metres

$$ {AC\over BC} = cos \ 60^0 ⇒ {x\over 19} = {1\over 2}⇒ x = {19\over 2} = 9.5 $$

∴ Distance of the root of the ladder from the wall = 9.5

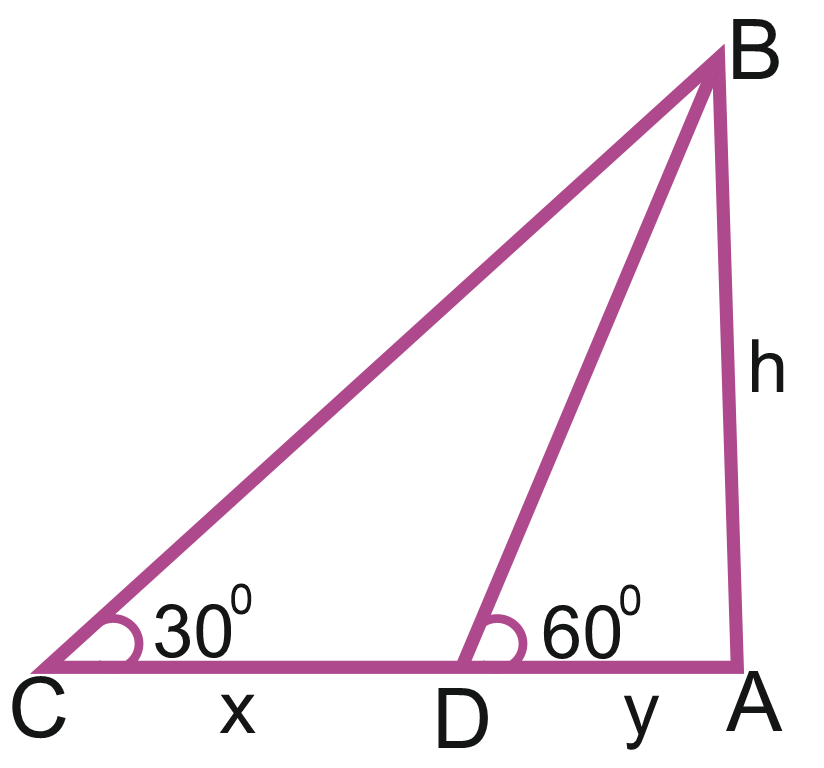
Ex.8. The angle of elevation of the top of a tower at a point on the ground is 30⁰ On walking 24 m towards the tower, the angle of elevation becomes 60⁰. Find the height of the tower.

$$Solution$$

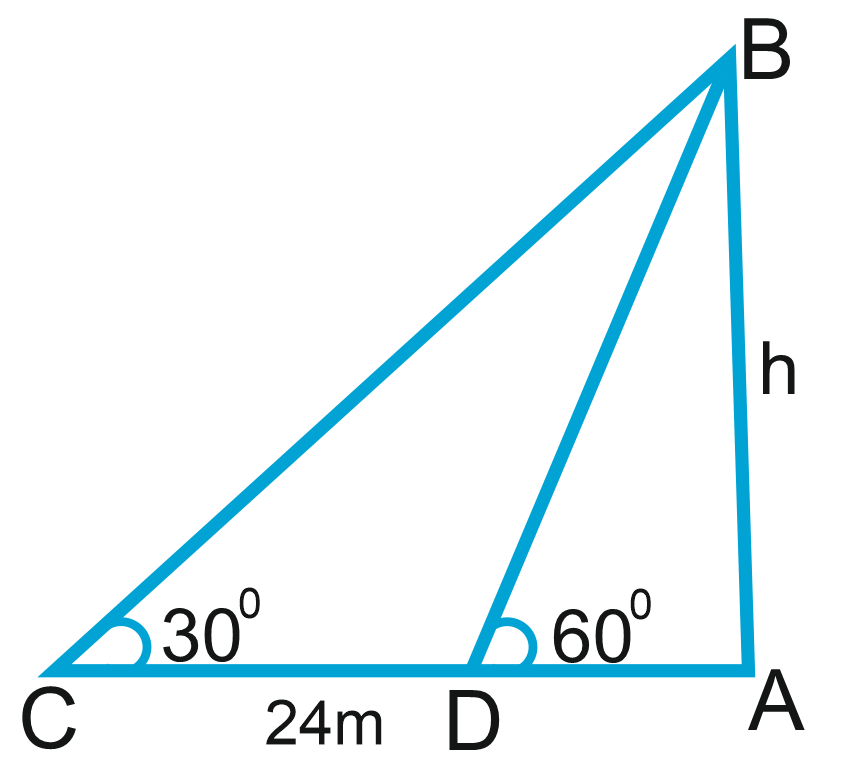
Let AB be the tower and C and D be the points of observation. Then,

$$ {AB\over AD} = tan \ 60^0 = \sqrt{3} ⇒ AD = {AD\over \sqrt{3}} = {h\over\sqrt{3}} $$

  $$ {AB\over AC} = tan \ 30^0 = {1\over \sqrt{3}}⇒ AC = AB× \sqrt{3}= h\sqrt{3} $$

  $$ CD = (AC - AD) = \left(h\sqrt{3} \ - {h\over \sqrt{3}}\right) $$

 $$ ∴ \ h\sqrt{3} \ - {h\over \sqrt{3}}= 24 ⇒ h = 12\sqrt{3}= (12×1.73)=20.76. $$

  Hence, the height of the tower is 20.76 m.

Ex.9. A man standing on the bank of a river observes that the angle subtended by tree on the opposite bank is 60⁰ When he retries 36 m from the bank, he finds the angle to be 30⁰. Find the breadth of the river. Find the breadth of the river.

$$Solution$$

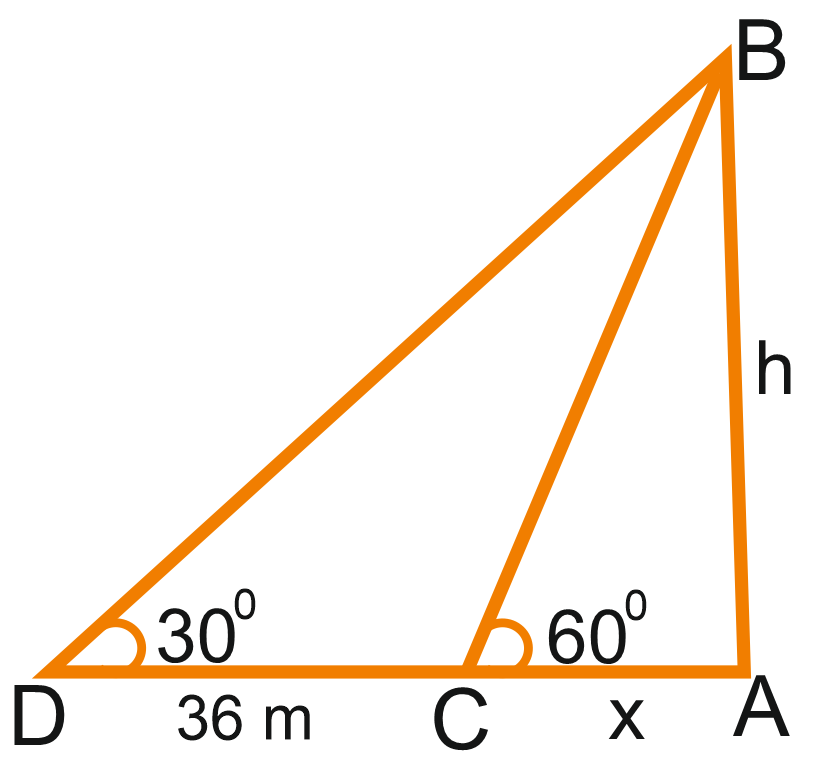
Let AB be the tree and AC be the river. Let C and D be the two position of the man. Then,

Then, ∠ABC = 60⁰, ∠ADB=30⁰  and CD = 36.

Let AB = h metres and AC = x metres.

Then, AD = (36+x) metres.

$$ {AB\over AD} = tan \ 30^0 = {1\over \sqrt{3}}⇒ {h\over 36+x}= {1\over \sqrt{3}} $$

  $$ ⇒ h = {36+x\over\sqrt{3}} ..........(i) $$ 

  $${AB\over AC} = tan \ 60^0 =  \sqrt{3} ⇒ {h\over x}= \sqrt{3} $$

  $$ ⇒ h = \sqrt{3}\ x ..........(ii) $$ 

  From (i) and (ii), we get :

  $$ {36+x \over\sqrt{3}}= \sqrt{3}⇒ x = 18 m. $$

So, the breadth of the river = 18 m.

Ex.10. A man on the top of a tower, standing on the seashore finds that a boat coming towards him takes 10 minutes for the angle of depression to change from 30⁰ to 60⁰. Find the time taken by the boat to reach the shore from this position.

$$Solution$$

Let AB be the tower and C and D be the two positions of the boat.

Let AB = h, CD = x and AD = Y.

$${h\over y} = tan \ 60^0 =   \sqrt{3} ⇒ y={h\over \sqrt{3}}$$

  $$ {h\over x+y}=tan \ 30^0 = {1\over{\sqrt{3}} } ⇒ x + y = \sqrt{3}\ h $$

  $$ ∴ \ x = (x+y)-y = \left(\sqrt{3}\ h \ - {h\over\sqrt{3}}\right)= {2h\over \sqrt{3}}$$

 $$ Now, {2h\over \sqrt{3}}\ is \ covered \ in \ 10 \ min$$

  $$∴ {{h\over \sqrt{3}} will \ be \ covered \ in \left(10×{\sqrt{3}\over2h}×{h\over\sqrt{3}}= 5 \ min\right) }$$

  Hence, required time = 5 minutes

I hope these formulas will helpful for your score high. You can ask me anything in the comment section related height and distance formulas with examples.