Logarithmic Equations and Examples with Solutions for SSC and Bank Exams

Logarithm quantitative aptitude questions asked in competitive exams often. Most of the students face difficulties while solving logarithmic problems because they don't practice logarithmic problems with solutions.
Here in this blog, you can simply resolve your difficulties of logarithmic problems with solutions. So try to solve logarithm problems own self easily and learn how to solve logarithm problems with solutions.
After learning you can more practice with logarithm questions with answers for ssc and bank exams and can improve your performance level also.
Logarithmic Problems with Solutions for Competitive Exams:
Logarithm equation examples and problems with solution
Q.1. The value of log343 7 is :
Solution
Let log343 7 = n. Then, (343)n = 7 ↔ (73)n = 7 ↔ 3n= 1
Q.2. The value of log√232 is :
Solution
Let log√232=n. Then, (√2)n=32↔(2)n/2=25
Q.3. The value of log(.01)(1000) is :
Solution
Let log(.01) (1000) = n.
Then, (.01)n = 1000
↔ (10-2n) = 103↔ - 2n=3
Q.4. if log3x = - 2, then x is equal to :
Solution
Log3x = -2 ↔ x = 3-2
Q.5. If logx ![]() =
= ![]() , then x is equal to :
, then x is equal to :
Solution
Q.6. The value of log2 16 is :
Solution
Let log2 16 = n. Then, 2n = 16 = 24→n=4.
∴ log2 16 = n.
Q.7. The value of log5 ![]() is :
is :
Solution
Q.8. The value of log10(.0001) is :
Solution
Let log10(.0001)=n.
Then, 10n = 0.001
↔ 10n=10–4 ↔ n = -4.
∴ log10 (.0001) =-4
Q.9. The logarithm of 0.0625 to the base 2 is :
Solution
Let log20.0625 = n. Then 2n = 0.0625
∴ log2 0.0625= - 4
Q10. If log8 x=  , then the value of x is :
, then the value of x is :
Solution
=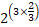 =22=4
=22=4
I hope these solutions are helpful for your preparation. If you have any problems or doubt regarding logarithmic equations examples and problems with solutions or you want ask any questions, you can ask me in the comment section.
All the best for your exam



