Probability Formulas with Examples for SSC and Bank PO

Most of the students are facing problems using formulas to solve probability questions in competitive exams. They only think about how they can use correctly probability formulas. If you also think the same in your mind, you can learn here how to use correctly probability formulas with examples. 

In this blog, you can obtain formulas of probability problems easily. You can practice Probability questions and answers also as well as learning the use of probability formulas with examples.

Probability formulas with examples for Competitive Exams

1. Experiment: An operation which can produced some well-defined outcomes is called an experiment.

2. Random Experiment: An experiment in which all possible outcomes are known and the exact output cannot be predicted in advance, is called a random experiment.

Examples of Performing a Random Experiment:

(A) Rolling an unbiased dice.

(B) Tossing a fair coin.

(C) Drawing a card from a pack of well-shuffled cards

(D) Picking up a ball of certain colour from a bag containing balls of different  Colours.

Details:

(A) When we throw a coin. Then either a Head (H) or Tail (T) appears.

(B) A dice is a solid cube, having 6 ices, marked 1, 2, 3, 4, 5, 6 respectively.

      When throw a die, the outcome is the number that appears on its upper face.

(C) A pack of cards has 52 cards.

      It has 13 cards of each suit, namely Spades, Clubs, Hearts and Diamonds.

     Cards of spades and clubs are black cards.

     There are 4 honours of each suit

     These are Aces, Kings, Queens and Jacks.

     These are called face cards.

3. Sample Space: When we perform an experiment, then the set S of all possible outcomes is called the Sample Space.

Examples of Sample Space:

(i) In tossing a coin, = S = {H, T}

(ii) If two cons are tossed, then S = {HH, HT, TH, TT}.

(iii) In rolling a dice, we have, S = [1,2,3,4,5,6].

4. Event: Any Subset of a sample space is called an event.

5. Probability of Occurrence of an Event: 

Let S be the sample space and let E be an event.

Then, E⊆S.

$$∴ P(E)={n(E)\over n(S)}. $$

6. Result on Probability :

(i) P (S) = 1            (ii) 0≤P (E) ≤ 1.         (iii) P (⏀) = 0 

(iv) For any events A and B, we have :

P (A ∪ B) = P(A) + P(B) – P ( A ∩ B)

(v) If 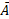 denotes (not-A), then P (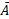) = 1 – P (A).

Example 

Ex.1. In a throw of coin, find the probability of getting a head.

Explanation  

Here S = {H, T} and E = {H}

$$∴ P(E)={n(E)\over n(S)} = {1\over2} $$

Ex.2. Two unbiased coins are tossed. What is the probability of getting a at most one head ?

Explanation  

Here S = {HH, TH, TT}.

Let E = event of getting at most one head.

∴ E = {TT, HT, TH}.

  $$∴ P(E)={n(E)\over n(S)} = {3\over4}$$

Ex.3. An unbiased die is tossed. Find the probability of getting a multiple of 3.

Explanation

Here S = {1,2,3,4,5,6}

Let E be the event of getting a multiple of 3.

Then, E = {3,6}

  $$∴ P(E)={n(E)\over n(S)} = {2\over6}={1\over3} $$

Ex.4. In a simultaneous throw of a pair of dice, find the probability of getting a total more than 7.

Explanation

Here, n (S) = (6×6) = 36.

Let E = Event of getting a total more than 7

= {(2,6), (3,5),(3,6),(4,4), (4,5), (4,6), (5,3), (5,4), (5,5), (5,6), (6,2), (6,3), (6,4), (6,5), (6,6)}

$$∴ P(E)={n(E)\over n(S)} = {15\over36}={5\over12} $$

Ex.5. Two dice are thrown together. What is the probability that the sum of the number on the two faces is divisible by 4 or 6?

Explanation

Clearly, n (S) = 6×6=36.

Let E be the event that the sum of the numbers on the two faces is divisible by 4 or 6. Then

E = { (1,3), (1,5), (2,2), (2,4), (2,6), (3,1), (3,3), (3,5), (4,2), (4,4), (5,1), (5,3), (6,2), (6,6)}

∴ n(E) = 14.

$$ Hence, \  P(E)={n(E)\over n(S)} = {14\over36}={7\over18} $$

I hope these formulas are helpful for you. If you have any problem and doubt or you want to ask me anything about probability formulas with examples, you can ask me in the comment box.

All the best.