Quantitative Aptitude Shortcut Tricks and Methods for Competitive Exam

Shortcut Tricks and Methods of Quantitative Aptitude:

Q.15. If I walk at 5km/h, I miss a train by 7 min. However, if I walk at 6 km/h I reach the station 5 min before the departure of the train. The distance between my house and the station is 

Solution  

Let the distance between my house and the station be d m.

Difference in time = 7+5=12 min.

⸫ d/5 – d/6 = 12/60 [∵ 1 min = 1/60 h]

→ 6d – 5d/30 = 1/5

→ d = 30/5 = 6 km

Q.16. The value of 204 * 197 is 

Solution

We have

204*197= (200+4)(200-3)

= 200(200-3)+4(200-3)

= 40000-600+800-12

=40800-612

=40188

Q.17. If p = 99, then the value of p (p²+3p+3) is 

Solution

Here, P = 99

⸫ P(P²+3p+3) = 99[(99)²+3*99+3]

=(100-1)[100-1]²+3(100-1)+3]

= (100-1) [10000+1-200+300-3+3]

= (100-1)[10000+101]

=(100-1)(10101)

=1010100-10101=999999

Q.18. In two similar triangles ABC and MNP, if AB = 2.25 cm, MP = 4.5 cm and PN = 7.5 cm and m∠MNP and m∠ABC = m ∠MPN, then the length of side BC, (in cm) is 

Solution

Here, ∆ABC ~ ∆MNP

⸫ AB/MP = BC/NP → 2.25/4.5 = BC/7.5

→ BC = [(2.25*7.5)/4.5]

= 16.875/4.5

= 3.75 cm

Q.19. Given an equilateral ∆ABC, D, E, F are the mid-point of AB, BC and AC respectively. Then, the quadrilateral BEFD is exactly a 

Solution

Given, an equilateral ∆ABC, in which D, E and F are the mid-points of AB, BC and AC, respectively.

So, all the sides are equal of ∆DEF which is the interior of an equilateral triangle ∆ABC.

i.e. DF = BE and DF||BE

DB= EF and DB|| EF

The quadrilateral BEFD is exactly a rhombus.

Q.20. If ABCD is cyclic parallelogram, then the ∠A is 

Solution

A quadrilateral is called cyclic if all the four vertices of it on a circle and opposite sides are parallel and sum of opposite angle of a cyclic quadrilateral is 180⁰

i.e AB|| CD and BD || AD  and ∠A+∠C = 180⁰.

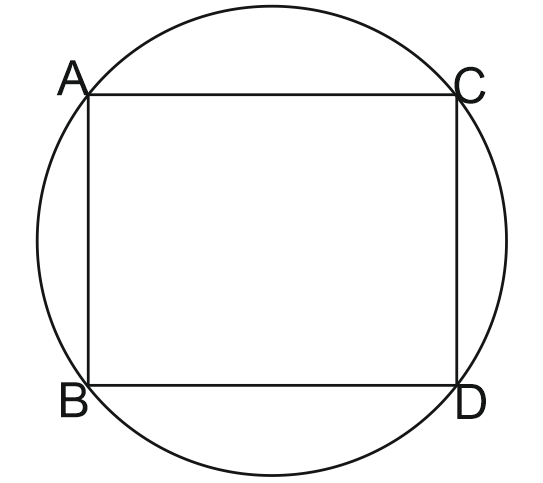
and ∠B+∠D = 180⁰ But, ABCD is a cyclic parallelogram,

⸫ ∠A=∠C = 90⁰

Without any hesitation, you can ask me anything in the comment section related quantitative aptitude shortcut tricks and methods.