Non Verbal Reasoning Practice Question and Answer
8 Q: Find the number of square?
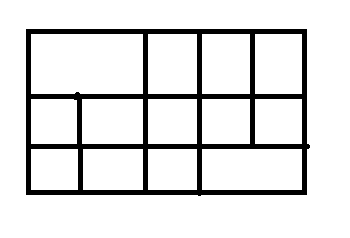
3446 05d2c1f2a2bb9b81db4a97d2e
5d2c1f2a2bb9b81db4a97d2e
- 110false
- 216false
- 319true
- 412false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 3. "19"
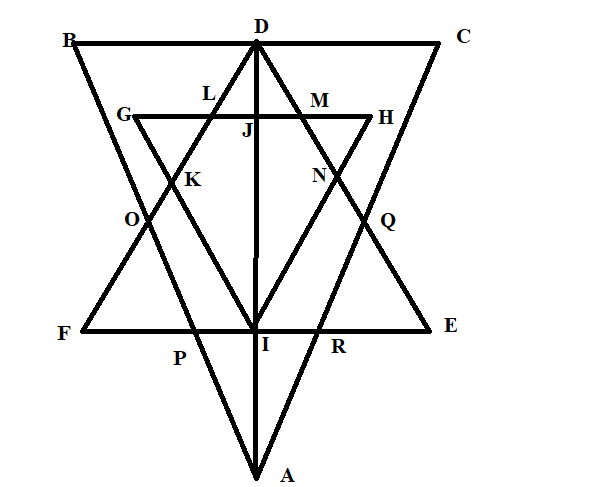
Q: In the question find the number of triangles.

14320 05d2c47732bb9b81db4a97f02
5d2c47732bb9b81db4a97f02
- 127true
- 225false
- 323false
- 421false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "27"
Explanation :
In the figure the simplest Triangles are GLK, DLJ, DJM,HMN,QRE,IRA,IPA, and FPO is the 8 triangle
and another is BDO,CDQ,DLM, PRA, KFI, NEI, HJI, GJI,DKI, and DNI is the 10 triangle
and another is DIE, DFI, DOA, DQA, and GHI is the 5 triangle
and DCA, DBA is the 2 triangle and DEF and ABC so that according to the figure the total no. of triangle is 8+10+5+2+1+1=27
Q: Determine the number of rectangles and hexagons in the following figure. 4775 35b5cc7b0e4d2b41977750821
5b5cc7b0e4d2b41977750821- 130, 5true
- 232, 3false
- 328, 5false
- 430, 3false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "30, 5"
Explanation :
Answer: A) 30, 5 Explanation: The figure may be labelled as shown Rectangles : The simplest rectangles are CVSR, VETS, RSWM and STKW i.e 4 in number. The rectangles composed of two components each are CETR, VEKW, RTKM and CVWM i.e 4 in number. The rectangles composed of three components each are ACRP, PRMO, EGHT and THIK i.e 4 in number. The rectangles composed of four components each are CEKM, AVSP, PSWO,VGHS and SHIW i.e 5 in number. The rectangles composed of five components each are AETP, PTKO, CGHR and RHIM i.e 4 in number. The rectangles composed of six components each are ACMO and EGIK i.e 2 in number. The rectangles composed of eight components each are AGHP, PHIO, AVWO and VGIW i.e 4 in number. The rectangles composed of ten components each are AEKO and CGIM i.e 2 in number. AGIO is the only rectangle having sixteen components Total number of rectangles in the given figure = 4 + 4 + 4 + 5 + 4 + 2 + 4 + 2 + 1 = 30. Hexagons : The hexagons in the given figure are CDEKLM, CEUKMQ, CFHJMQ, BEUKNP and BFHJNP. So, there are 5 hexagons in the given figure.
Q: How many squares in the figure?
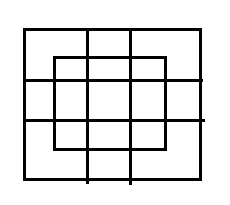
6248 05d2c22de2bb9b81db4a97d3d
5d2c22de2bb9b81db4a97d3d
- 116false
- 218false
- 325false
- 427true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "27"
Explanation :
In this figure counting the squares and we get the 27 squares.
Q: When two dice are thrown simultaneously, what is the probability that the sum of the two numbers that turn up is less than 12? 2444 05b5cc5ffe4d2b4197774b427
5b5cc5ffe4d2b4197774b427- 135/36true
- 217/36false
- 315/36false
- 41/36false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "35/36"
Explanation :
Answer: A) 35/36 Explanation: When two dice are thrown simultaneously, the probability is n(S) = 6x6 = 36 Required, the sum of the two numbers that turn up is less than 12 That can be done as n(E) = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6)(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)(6,1), (6,2), (6,3), (6,4), (6,5) } = 35 Hence, required probability = n(E)/n(S) = 35/36.
Q: Two dice are rolled simultaneously. Find the probability of getting a total of 9. 2975 05b5cc7d1e4d2b41977751268
5b5cc7d1e4d2b41977751268- 11/3false
- 21/9true
- 38/9false
- 49/10false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 2. "1/9"
Explanation :
Answer: B) 1/9 Explanation: S = { (1, 1), (1, 2), (1, 3), (1, 4),(1, 5), (1, 6), (2, 1), (2, 2),.........(6, 5), (6, 6) } => n(S) = 6 x 6 = 36 E = {(6, 3), (5, 4), (4, 5), (3, 6) } => n(E) = 4 Therefore, P(E) = 4/36 = 1/9
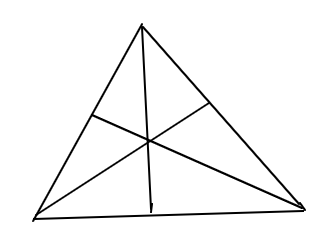
Q: Find the number of triangles ?
5923 05d2c0a4640a93b3eb992dba5
5d2c0a4640a93b3eb992dba5
- 116true
- 213false
- 39false
- 47false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "16"
Explanation :
3+3+3=9 triangle
Triangle ABD +Triangle ADC =2
Same as 2+2+2=6
And Triangle ABC=1
So that total no of triangle in this figure is 9+6+1=16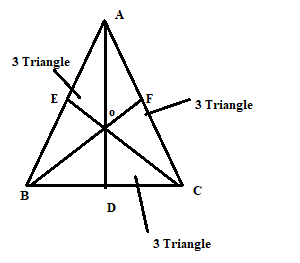
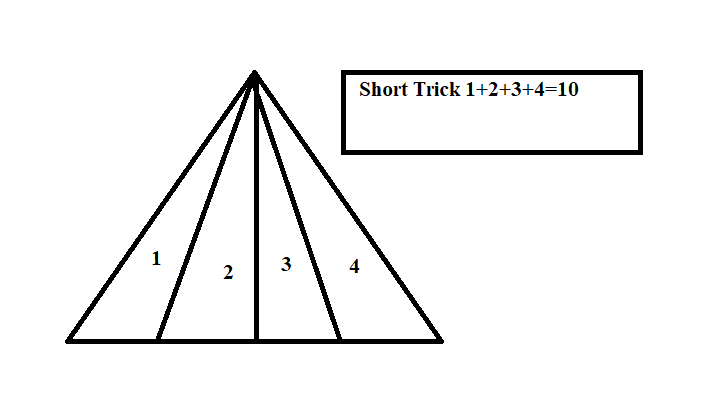
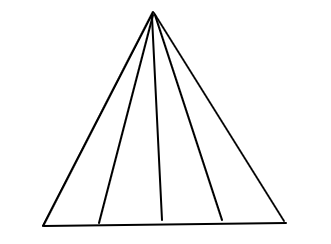
Q: How many triangle is in the given figure?
6257 05d2c273440a93b3eb992dc38
5d2c273440a93b3eb992dc38
- 110true
- 212false
- 314false
- 416false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "10"
Explanation :