Non Verbal Reasoning Practice Question and Answer
8 Q: How many squares are there in the following figure?
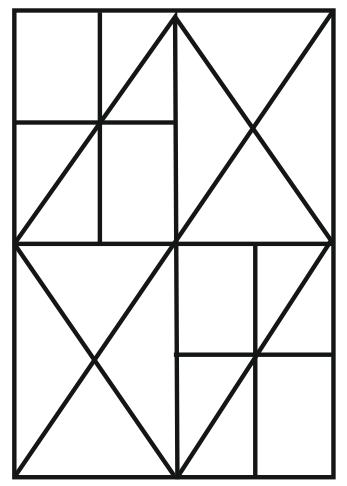
2224 05da6dacad8305e690883ca59
5da6dacad8305e690883ca59
- 114true
- 213false
- 312false
- 416false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "14"
Q: Determine the number of rectangles and hexagons in the following figure. 4186 35b5cc7b0e4d2b41977750821
5b5cc7b0e4d2b41977750821- 130, 5true
- 232, 3false
- 328, 5false
- 430, 3false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "30, 5"
Explanation :
Answer: A) 30, 5 Explanation: The figure may be labelled as shown Rectangles : The simplest rectangles are CVSR, VETS, RSWM and STKW i.e 4 in number. The rectangles composed of two components each are CETR, VEKW, RTKM and CVWM i.e 4 in number. The rectangles composed of three components each are ACRP, PRMO, EGHT and THIK i.e 4 in number. The rectangles composed of four components each are CEKM, AVSP, PSWO,VGHS and SHIW i.e 5 in number. The rectangles composed of five components each are AETP, PTKO, CGHR and RHIM i.e 4 in number. The rectangles composed of six components each are ACMO and EGIK i.e 2 in number. The rectangles composed of eight components each are AGHP, PHIO, AVWO and VGIW i.e 4 in number. The rectangles composed of ten components each are AEKO and CGIM i.e 2 in number. AGIO is the only rectangle having sixteen components Total number of rectangles in the given figure = 4 + 4 + 4 + 5 + 4 + 2 + 4 + 2 + 1 = 30. Hexagons : The hexagons in the given figure are CDEKLM, CEUKMQ, CFHJMQ, BEUKNP and BFHJNP. So, there are 5 hexagons in the given figure.
Q: In the following question number of triangle are
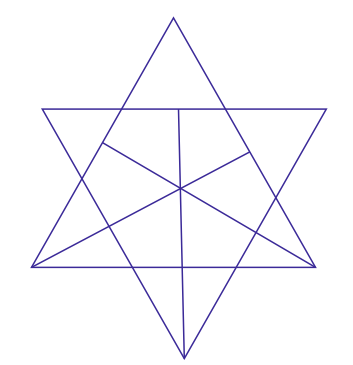
19314 05d2c4d440272a3586d3b5048
5d2c4d440272a3586d3b5048
- 121false
- 223false
- 325false
- 427true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "27"
Explanation :
The main triangle shown is in the given figure and this the total no. of triangle is 15. remaing triangle we can find out in the drawing the triangle in the image.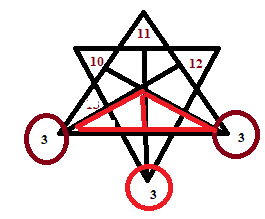
Q: When two dice are thrown simultaneously, what is the probability that the sum of the two numbers that turn up is less than 12? 1814 05b5cc5ffe4d2b4197774b427
5b5cc5ffe4d2b4197774b427- 135/36true
- 217/36false
- 315/36false
- 41/36false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "35/36"
Explanation :
Answer: A) 35/36 Explanation: When two dice are thrown simultaneously, the probability is n(S) = 6x6 = 36 Required, the sum of the two numbers that turn up is less than 12 That can be done as n(E) = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6)(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)(6,1), (6,2), (6,3), (6,4), (6,5) } = 35 Hence, required probability = n(E)/n(S) = 35/36.
Q: Two dice are rolled simultaneously. Find the probability of getting a total of 9. 2194 05b5cc7d1e4d2b41977751268
5b5cc7d1e4d2b41977751268- 11/3false
- 21/9true
- 38/9false
- 49/10false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 2. "1/9"
Explanation :
Answer: B) 1/9 Explanation: S = { (1, 1), (1, 2), (1, 3), (1, 4),(1, 5), (1, 6), (2, 1), (2, 2),.........(6, 5), (6, 6) } => n(S) = 6 x 6 = 36 E = {(6, 3), (5, 4), (4, 5), (3, 6) } => n(E) = 4 Therefore, P(E) = 4/36 = 1/9
Q: Find the number of triangles ?
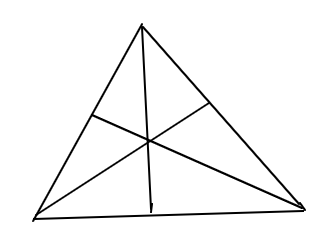
5247 05d2c0a4640a93b3eb992dba5
5d2c0a4640a93b3eb992dba5
- 116true
- 213false
- 39false
- 47false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "16"
Explanation :
3+3+3=9 triangle
Triangle ABD +Triangle ADC =2
Same as 2+2+2=6
And Triangle ABC=1
So that total no of triangle in this figure is 9+6+1=16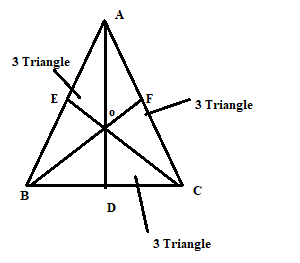
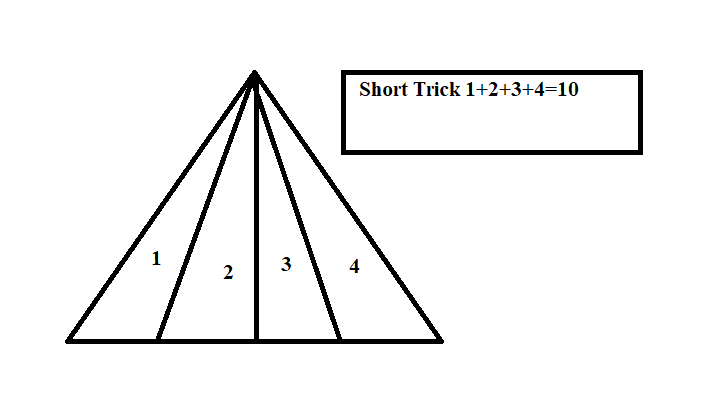
Q: How many triangle is in the given figure?
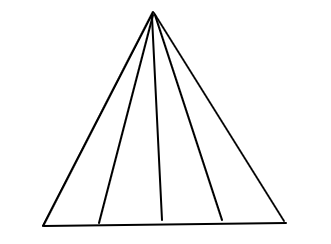
5396 05d2c273440a93b3eb992dc38
5d2c273440a93b3eb992dc38
- 110true
- 212false
- 314false
- 416false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "10"
Explanation :
Q: Choose a figure which would most closely resemble the unfolded form of Figure (Z).

6210 05d789fa40c830b6303aecf5a
5d789fa40c830b6303aecf5a
- 11false
- 22true
- 33false
- 44false
- Show AnswerHide Answer
- Workspace
- SingleChoice

