Number System Questions Practice Question and Answer
8 Q: 64329 is divided by a certain number. While dividing, the numbers, 175, 114 and 213 appear as three successive remainders. The divisor is?
783 06220c43360ee9a48009afe5b
6220c43360ee9a48009afe5b- 1184false
- 2224false
- 3234true
- 4296false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "234 "
Explanation :
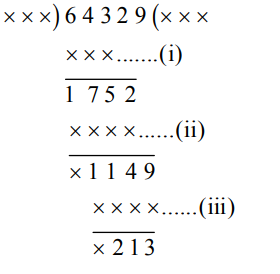
Number at (i) = 643 – 175 = 468
Number at (ii) = 1752 – 114 = 1638
Number at (iii) = 1149 – 213 = 936
Clearly, 468, 1638 and 936 are multiples of 234 and 234 > 213.
Divisor = 234
Q: A number divided by 13 leaves a remainder 1 and if the quotient, thus obtained, is divided by 5, we get a remainder of 3. What will be the remainder if the number is divided by 65?
1232 05d7f1ae6fb24f902086364bb
5d7f1ae6fb24f902086364bb- 128false
- 216false
- 318false
- 440true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "40"
Explanation :
Let the least number be x
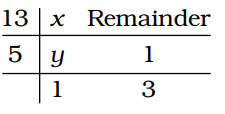
y = 5 × 1 + 3 = 8
x = 13 × 8 + 1 = 105
On dividing 105 by 65, remainder = 40
Q: A number when divided by 6 leaves remainder 3. When the square of the same number is divided by 6, the remainder is :
508 0650d36e3d2f211504875ecda
650d36e3d2f211504875ecda- 10false
- 21false
- 32false
- 43true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "3"
Explanation :
The remainder will be same.
On dividing 9 by 6, remainder = 3
On dividing 81 by 6, remainder = 3
Q: A number when divided by 119, leaves a remainder of 19. If it is divided by 17, it will leave a remainder of:
912 0614c68834d59797c590e504e
614c68834d59797c590e504e- 119false
- 27false
- 310false
- 42true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "2 "
Explanation :
On dividing the given number by 119, let k be the quotient and 19 as remainder.
Then, number = 119k + 19
= 17 × 7k + 17 × 1 + 2
= 17 (7k + 1) + 2
Hence, the given number when divided by 17, gives (7k + 1) as quotient and 2 as remainder.
Q: How many natural numbers divisible by 7 are there between 3 and 200?
1069 05ee845d3a08a50198d8d094c
5ee845d3a08a50198d8d094c- 128true
- 229false
- 327false
- 436false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "28 "
Explanation :
Number just greater than 3 which is divisible by 7 = 7
Number just smaller than 200 which is divisible by 7 = 196
Here, a = 7, an = 196,
d = 7, n = 8
an = a + (n –1)d
⇒196 = 7 + (n – 1) × 7
⇒ 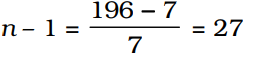
⇒ n = 27 + 1 = 28
Note : We can find the answer after dividing 200 by 7. The quotient is our answer.
Q: Each member of a Picnic party contributed twice as many rupees as the total collection was Rs.3042. The number of members present in the party was
1000 05ec4a257980ff60a66c06591
5ec4a257980ff60a66c06591- 12false
- 232false
- 342false
- 439true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "39"
Explanation :
Let the required number of persons be x.
According to the question, 2x2 = 3042
Or 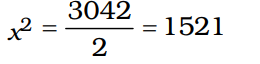
or 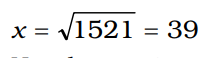
Q: A number when divided by 296 gives a remainder 75. When the same number is divided by 37 the remainder will be:
966 05ee8426479b5ea388bec0116
5ee8426479b5ea388bec0116- 18false
- 21true
- 32false
- 411false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "1 "
Explanation :
Let number (dividend) be X.
∴ X = 296 × Q + 75 where Q is the quotient and can have the values 1, 2, 3 etc.
= 37 × 8 × Q + 37 × 2 + 1
= 37 (8Q + 2) + 1
Thus we see that the remainder is 1.
[Remark : When the second divisor is a factor of the first divisor, the second remainder is obtained by dividing the first remainder by the second divisor.
Hence, divide 75 by 37, the remainder is 1].
Q: When 1062, 1134 and 1182 are divided by the greatest number .x, the remainder in each case is y. What is the value of (x − y)?
724 064ba4fa5c3da05b2213e134d
64ba4fa5c3da05b2213e134d- 117false
- 218true
- 316false
- 419false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "18"
Explanation :


The value of (x-y) will be 18

