Number System Questions Practice Question and Answer
8 Q: Which of the following statements is a false statement?
(A) CRT The monitor is the thinnest monitor.
(B) Dot matrix is the fastest computer.
(C) CAG memory is slower than the main memory.
(D) Bar code reader is an input device.
815 064b920e8568e7ff594be2e6b
64b920e8568e7ff594be2e6b- 1a and bfalse
- 2a, b and ctrue
- 3c and dfalse
- 4a and dfalse
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 2. "a, b and c"
Explanation :
All statements are true.
- CRT The monitor is the thinnest monitor.
- Dot matrix is the fastest computer.
- CAG memory is slower than the main memory.
Q: Which of the following fraction is the smallest?
$$7\over 6 $$,$$7\over 9$$,$$4\over 5$$,$$5\over 7$$
781 065081b75e918d9427f49639d
65081b75e918d9427f49639d- 1$$7\over 6 $$false
- 2$$7\over 9$$false
- 3$$4\over 5$$false
- 4$$5\over 7$$true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "$$5\over 7$$"
Explanation :

Q: A number when divided by 192 gives a remainder of 54. What remainder would be obtained on dividing the same number by 16 ?
1016 0650d458363078e50a2943253
650d458363078e50a2943253- 12false
- 24false
- 36true
- 48false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 3. "6"
Explanation :
Here, the first divisor 192 is a multiple of second divisor 16.
∴ Required remainder
= remainder obtained by dividing 54 by 16 = 6
Q: A number when divided by 5 leaves a remainder 3. What is the remainder when the square of the same number is divided by 5 ?
979 0650d43a2cb11fc5036d68479
650d43a2cb11fc5036d68479- 11false
- 22false
- 33false
- 44true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "4"
Q: A number consists of two digits. If the number formed by interchanging the digits is added to the original number, the resulting number (i.e. the sum) must be divisible by
929 0650d423410a18f5082eccafc
650d423410a18f5082eccafc- 111true
- 29false
- 35false
- 43false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "11"
Explanation :
Let the number be 10x + y
After interchanging the digits,
the number obtained = 10y + x
According to the question,
Resulting number
= 10x + y + 10y + x
= 11x + 11y
= 11 (x + y)
which is exactly divisible by 11.
Q: If two numbers are each divided by the same divisor, the remainders are respectively 3 and 4. If the sum of the two numbers be divided by the same divisor, the remainder is 2. The divisor is
1002 0650d401473357650645d2108
650d401473357650645d2108- 19false
- 27false
- 35true
- 43false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 3. "5 "
Explanation :
Required divisor = 3 + 4 – 2 = 5
Q: In a question on division, the divisor is 7 times the quotient and 3 times the remainder. If the remainder is 28, then the dividend is
824 0650d3f3f73357650645d20e3
650d3f3f73357650645d20e3- 1588false
- 2784false
- 3823false
- 41036true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "1036"
Explanation :
Let the quotient be Q and the remainder be R. Then
Divisor = 7 Q = 3 R
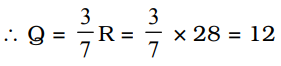
∴ Divisor = 7 Q = 7 × 12 = 84
Dividend = Divisor × Quotient + Remainder = 84 × 12 + 28 = 1008 + 28 = 1036
Q: 64329 is divided by a certain number, 175, 114 and 213 appear as three successive remainders. The devisor is
2121 05d91f524a01ffd5718894157
5d91f524a01ffd5718894157- 1184false
- 2224false
- 3234true
- 4296false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 3. "234"
Explanation :
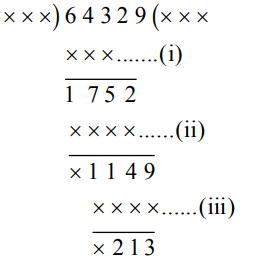
Number at (i) = 643 – 175 = 468
Number at (ii) = 1752 – 114 = 1638
Number at (iii) = 1149 – 213 = 936
Clearly, 468, 1638 and 936 are multiples of 234 and 234 > 213.
Divisor = 234

