Cubes and Dice Practice Question and Answer
8 Q: Position of Dices are given below:
Identify the number when top is 5 what will be at bottom?
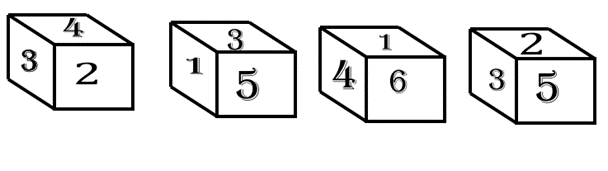
1849 16257c6580560954965a64004
6257c6580560954965a64004
- 16false
- 23false
- 34true
- 42false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "4"
Q: A cuboid whose length is 6 cm. width 4 cm. and height 1 cm. Is.Two faces measuring 4 cm. x1 cm. It is painted black. Two fruits measuring 6 cm. x1 cm. is painted red and is 6 cm. x4 cm. The two faces are painted green. This cuboid is divided by 1 cm. x1 cm. x1 cm. How many cubes have green color on two faces and no color on the remaining four faces -
1647 0619b91efc1c85f0fbf3b2508
619b91efc1c85f0fbf3b2508- 112false
- 28true
- 310false
- 44false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "8"
Q: A cuboid whose length is 6 cm. width 4 cm. and height 1 cm. Is. Two faces measuring 4 cm. x 1 cm. It is painted black. Two faces measuring 6 cm. x 1 cm. is painted red and is 6 cm. x 4 cm. The two faces are painted green. This cuboid is divided by 1 cm. x1 cm. x1 cm. is cut into cubes, then if the faces containing black and green are removed, then how many cubes will remain -
1474 0619b8d6a925df30febe30861
619b8d6a925df30febe30861- 18false
- 24false
- 316true
- 412false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "16"
Q: A solid cube is made using 64 small cubes. How many of these small cubes are not visible at all -
2184 0619b9053925df30febe30dcd
619b9053925df30febe30dcd- 16false
- 24false
- 32false
- 48true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "8"
Q: When two dice are thrown simultaneously, what is the probability that the sum of the two numbers that turn up is less than 12? 2098 05b5cc5ffe4d2b4197774b427
5b5cc5ffe4d2b4197774b427- 135/36true
- 217/36false
- 315/36false
- 41/36false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "35/36"
Explanation :
Answer: A) 35/36 Explanation: When two dice are thrown simultaneously, the probability is n(S) = 6x6 = 36 Required, the sum of the two numbers that turn up is less than 12 That can be done as n(E) = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6)(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)(6,1), (6,2), (6,3), (6,4), (6,5) } = 35 Hence, required probability = n(E)/n(S) = 35/36.
Q: In a big cube, there are only two faces colored total cubes are 24. Find out how many small cubes are there in this big cube?
1772 060be0129943add67dd72fae1
60be0129943add67dd72fae1- 164true
- 224false
- 3125false
- 4343false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "64"
Q: Two dice are rolled simultaneously. Find the probability of getting a total of 9. 2471 05b5cc7d1e4d2b41977751268
5b5cc7d1e4d2b41977751268- 11/3false
- 21/9true
- 38/9false
- 49/10false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "1/9"
Explanation :
Answer: B) 1/9 Explanation: S = { (1, 1), (1, 2), (1, 3), (1, 4),(1, 5), (1, 6), (2, 1), (2, 2),.........(6, 5), (6, 6) } => n(S) = 6 x 6 = 36 E = {(6, 3), (5, 4), (4, 5), (3, 6) } => n(E) = 4 Therefore, P(E) = 4/36 = 1/9
Q: In a big cube, only two surface-colored total cubes are 24. Find out how many total small cubes are there in this big cube?
1489 06078f76f63b9781494e74464
6078f76f63b9781494e74464- 164true
- 224false
- 3125false
- 4343false
- Show Answer
- Workspace
- SingleChoice

