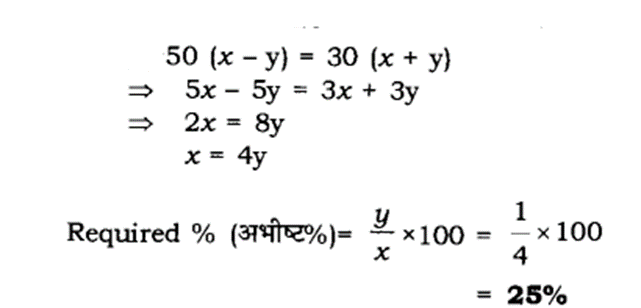Percentage Practice Question and Answer
8 Q: If the population of a town is 12.000 and the population increases at the rate of 10% per annum, then find the population. after 3 years.
798 06426e27c72ca731a990e28e2
6426e27c72ca731a990e28e2- 115,972true
- 212,200false
- 311,200false
- 410,200false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "15,972"
Explanation :
To find the population after 3 years given that it increases at a rate of 10% per annum, you can use the formula for exponential growth:
𝑃=𝑃0×(1+𝑟)𝑛P=P0×(1+r)n
Where:
- 𝑃P = Population after 𝑛n years
- 𝑃0P0 = Initial population
- 𝑟r = Rate of increase (in decimal form)
- 𝑛n = Number of years
Given:
- 𝑃0=12,000P0=12,000 (Initial population)
- 𝑟=0.10r=0.10 (10% increase per annum)
- 𝑛=3n=3 (Number of years)
Substitute these values into the formula:
𝑃=12,000×(1+0.10)3P=12,000×(1+0.10)3
𝑃=12,000×(1.10)3P=12,000×(1.10)3
𝑃=12,000×(1.331)P=12,000×(1.331)
𝑃=15,972P=15,972
So, the population after 3 years would be approximately 15,972.
Q: The price of sugar increases by 15%. By what percentage should the consumption of sugar be decreased so that the expenditure on the purchase of sugar remains the same? [Give your answer correct to 2 decimal places.]
799 0643d140332185cce373eec85
643d140332185cce373eec85- 111.11%false
- 212.5%false
- 314.16%false
- 413.04%true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "13.04%"
Explanation :
To solve this problem, let's denote:
- Initial price of sugar = P
- Initial quantity consumed = Q
- Initial expenditure = PQ
After the price increases by 15%, the new price becomes 1.15P.
To keep the expenditure constant, the new quantity consumed (let's call it Q') can be calculated using the formula:
New expenditure = New price × New quantity
Setting the new expenditure equal to the initial expenditure:
PQ = (1.15P) * Q'
Now, solve for Q':
Q' = PQ / (1.15P)
Simplify:
Q' = Q / 1.15
Now, let's find the percentage decrease in consumption:
Percentage decrease = [(Q - Q') / Q] * 100
Substituting the value of Q':
Percentage decrease = [(Q - (Q / 1.15)) / Q] * 100
Percentage decrease = [(Q * (1 - 1/1.15)) / Q] * 100
Percentage decrease ≈ [(1 - 0.8696) * 100] ≈ 13.04%
Therefore, the consumption of sugar should be decreased by approximately 13.04% to keep the expenditure on the purchase of sugar the same after a 15% increase in price.
Q: In an examination, 92% of the students passed and 480 students failed. If so, how many students appeared in the examination?
749 064cce0cd8f85ca71558f105f
64cce0cd8f85ca71558f105f- 15800false
- 26200false
- 36000true
- 45000false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "6000"
Explanation :
Let's denote the total number of students who appeared in the examination as 𝑥x.
Given that 92% of the students passed, it means 8% failed because the total percentage is 100%.
We can set up the equation:
8% of 𝑥=4808% of x=480To find 8% of 𝑥x, we multiply 𝑥x by 81001008 (which is the same as multiplying by 0.08):
0.08𝑥=4800.08x=480Now, we can solve for 𝑥x:
𝑥=4800.08x=0.08480𝑥=6000x=6000So, 6000 students appeared in the examination.
Q: The sum of weights of A and B is 80 kg. 50% of A's weight is
793 064ccef6ba919c8488e304799
64ccef6ba919c8488e304799- 120 kgtrue
- 210 kgfalse
- 325 kgfalse
- 415 kgfalse
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "20 kg"
Explanation :
Let's denote the weight of A as 𝑥x kg and the weight of B as 𝑦y kg.
Given:
- 𝑥+𝑦=80x+y=80 (Sum of weights of A and B is 80 kg)
- 0.5𝑥=56𝑦0.5x=65y (50% of A's weight is 5665 times the weight of B)
We can solve these two equations to find the values of 𝑥x and 𝑦y, and then calculate the difference between their weights.
From equation 2: 0.5𝑥=56𝑦0.5x=65y Multiply both sides by 2 to get rid of the fraction: 𝑥=56𝑦×2x=65y×2 𝑥=106𝑦x=610y 𝑥=53𝑦x=35y
Now substitute this expression for 𝑥x into equation 1: 53𝑦+𝑦=8035y+y=80 83𝑦=8038y=80 Multiply both sides by 3883: 𝑦=80×38y=80×83 𝑦=30y=30
Now that we have found the weight of B, we can find the weight of A using equation 1: 𝑥+30=80x+30=80 𝑥=80−30x=80−30 𝑥=50x=50
So, the weight of A is 50 kg and the weight of B is 30 kg.
Now, let's find the difference between their weights: Difference=Weight of A−Weight of BDifference=Weight of A−Weight of B Difference=50−30Difference=50−30 Difference=20Difference=20
Therefore, the difference between their weights is 20 kg.
Q: If 40% of (A+B) = 60% of (A-B) then
912 065424ed827398ecb26d95af5
65424ed827398ecb26d95af5- 1true
- 2false
- 3false
- 4false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "
Explanation :

Q: 0.15% of
473 0653f6eb2dfda58cb3c9373bf
653f6eb2dfda58cb3c9373bf- 1₹ 5true
- 2₹ 150false
- 3₹ 0.05false
- 4₹ 105false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "₹ 5"
Explanation :
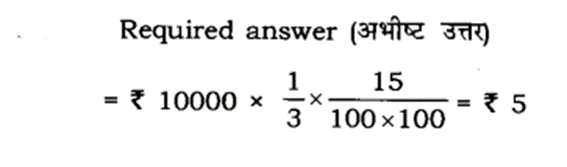
Q: If x% of
547 0653f7cb899dc28caf022bf23
653f7cb899dc28caf022bf23- 11000false
- 21200true
- 31400false
- 41500false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "1200"
Explanation :
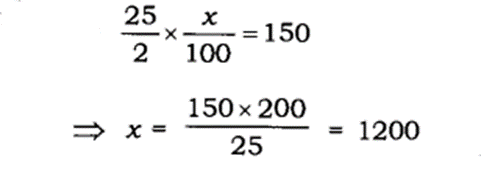
Q: if 50% of (x-y) =30% of (x+y), then what percentage of x is y?
514 0653f7d3bc298bbcb027eedf6
653f7d3bc298bbcb027eedf6- 125%true
- 2false
- 340%false
- 4400%false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "25%"
Explanation :