Algebra Question with answer Practice Question and Answer
8 4 Q:
5f1e9a361b4d8003eeb16c7f 4 Q:
5dca42ed582669277c292e29 4 Q:
5ec4a7b2980ff60a66c0683d Answer : 2. "
4 Q:
5d70dc5d60d0a53645a49df5 4 Q:
5d8c8e00e01f466533646b06 4 Q:
5dca43e8582669277c292f17 4 Q:
5ddcdd14e1ce690ab506aa1e 4 Q:
5ed62576ebc5ce408e2a9643
Q: If 5√x + 12√x = 13√x, then x is equal to:
857 05f1e9a361b4d8003eeb16c7f
5f1e9a361b4d8003eeb16c7f- 19false
- 216false
- 3$${25\over4}$$false
- 44true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "4"
Q: If average of two x and $$1\over x$$ (where x ≠ 0) is A, what will be the average of x3 and $$1\over {x^3}$$?
1099 05dca42ed582669277c292e29
5dca42ed582669277c292e29- 1$$4A^3-2A$$false
- 2$$4A^3-3A$$true
- 3$$4A^3-4A$$false
- 4$$4A^2-2A$$false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "$$4A^3-3A$$ "
Q: simplify the following equation
$$ (1-{1\over3})(1-{1\over4})(1-{1\over5})......(1-{1\over n})$$
862 05ec4a7b2980ff60a66c0683d
5ec4a7b2980ff60a66c0683d$$ (1-{1\over3})(1-{1\over4})(1-{1\over5})......(1-{1\over n})$$
- 1false
- 2true
- 3false
- 4false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "
Q: Solve the following equation.
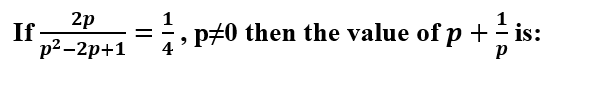
1136 05d70dc5d60d0a53645a49df5
5d70dc5d60d0a53645a49df5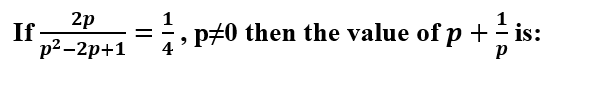
- 14false
- 25false
- 310true
- 412false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "10"
Q: If
1216 05d8c8e00e01f466533646b06
5d8c8e00e01f466533646b06- 1– 1true
- 20false
- 31false
- 42false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "– 1 "
Q: If x2+y2+z2 = xy + yz + zx, then the value of
1579 05dca43e8582669277c292f17
5dca43e8582669277c292f17- 12false
- 21true
- 30false
- 4-1false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "1"
Q: If
1277 05ddcdd14e1ce690ab506aa1e
5ddcdd14e1ce690ab506aa1e- 1110false
- 2115true
- 3125false
- 4120false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "115"
Q: If x = 2 then the value of
1389 05ed62576ebc5ce408e2a9643
5ed62576ebc5ce408e2a9643- 11211false
- 21231false
- 31233true
- 41321false
- Show Answer
- Workspace
- SingleChoice

