Trigonometry Practice Question and Answer
8 4 Q:
5f0e7590f4c8bf4bad0034fc 4 Q:
5f06dd933f7f07047795e991 Answer : 2. "$$ tanθ+cotθ$$"
4 Q:
5f058db23f7f070477919df3 Answer : 1. "
4 Q:
5efeb11c7228dd6b06e74e29 Answer : 1. "
4 Q:
5efeafe79bfe193cd14b75c5 Answer : 2. "
4 Q:
5efeaf90d4461c5b47dceb30 Answer : 2. "
4 Q:
5ef04e7e8022cc4acbba8b20 Answer : 3. "
4 Q:
5ef04da781a47f2e7ae446be Answer : 2. "
Q: If sec -5π/4 = x, then the value of x is
1112 05f0e7590f4c8bf4bad0034fc
5f0e7590f4c8bf4bad0034fc- 1-1/√3false
- 2-√2true
- 3-1false
- 4√3false
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "-√2"
Q: $$ \sqrt {sec^2{θ}+cosec^2{θ}}=?$$
1361 05f06dd933f7f07047795e991
5f06dd933f7f07047795e991- 1$$ {tan^2{θ}}+cot^2{θ}$$false
- 2$$ tanθ+cotθ$$true
- 3$$ sinθ+cosθ$$false
- 4None of thesefalse
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "$$ tanθ+cotθ$$"
Explanation :
$$ \sqrt {sec^2{θ}+cosec^2{θ}}$$
We know that
$$ {1+tan^2{θ}}={sec^2θ}$$
$$ {1+cot^2{θ}}={cosec^2{θ}}$$
$$ \sqrt {1+tan^2{θ}+1+cot^2{θ}}$$
Q: If θ θ θ θ
954 05f058db23f7f070477919df3
5f058db23f7f070477919df3- 1true
- 2false
- 3false
- 4false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "
Q: θ
986 05efeb11c7228dd6b06e74e29
5efeb11c7228dd6b06e74e29- 1true
θ - 2false
θ - 3false
θ - 4false
θ
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "θ
Q:
1015 05efeafe79bfe193cd14b75c5
5efeafe79bfe193cd14b75c5- 10false
- 2true
- 3false
- 4None of thesefalse
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "
Q: If 4tanθ=3,the value of θ θ θ θ
1210 05efeaf90d4461c5b47dceb30
5efeaf90d4461c5b47dceb30- 1false
- 2true
- 3false
- 4None of thesefalse
- Show Answer
- Workspace
- SingleChoice
Answer : 2. "
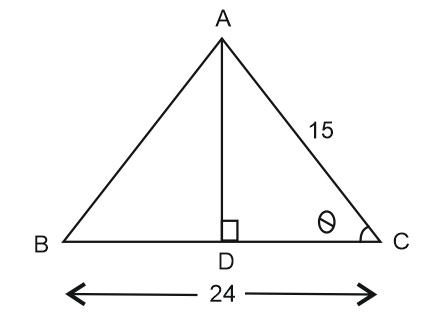
Q: Find the value tanθ-cosθ in the given figure.
1425 05ef04e7e8022cc4acbba8b20
5ef04e7e8022cc4acbba8b20
- 1false
- 2false
- 3true
- 4false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "
Q: Find the value of
1278 05ef04da781a47f2e7ae446be
5ef04da781a47f2e7ae446be- 1false
- 2true
- 30false
- 4false
- Show Answer
- Workspace
- SingleChoice

